Publications
My primary research interest is in probability, specifically in the study of spin systems, random graphs, Gibbs measures, and other topics related to statistical physics. Below you will find a list of my publications, accompanied by short descriptions (click to show/hide) of the relevant context and main results.
6. Decoupling of clusters in independent sets in a percolated hypercube
This is a followup to our previous work on independent sets: 2410.07080; please refer to the description for it (below) for the broad context. In this work, the focus is on resolving the case when the defects start to interact, below $p \leq 2 - \sqrt{2}$. In fact, our techniques are powerful enough to push the results all the way down to $p \geq 0.47$, notably across the critical threshold $p = 0.5$ for many other models on the hypercube.
We defer a more technical description to the preprint itself.
5. Spectral properties of the zero temperature Edwards-Anderson model
Models of spin glasses have been extensively studied in statistical physics, and, after a series of groundbreaking results, we have a reasonably complete understanding of the simplest of these models -- the Sherrington-Kirkpatrick (SK) model: see this survey for instance. However, the SK model is only a crude approximation of the realistic Edwards-Anderson (EA) model on a lattice, an object notoriously intractable, even in the physics literature. Only recently has there been some progress on the rigorous side due to Sourav Chatterjee, see the preprint. In our work, we introduce probabilistic ideas into the mix, allowing us to develop the first bounds on the spectral sample that exhibit growth more than what is implied by direct connectivity arguments. This is also a step towards establishing the conjectural superlinear lower bounds on the spectral sample.
4. Invariance principle for the Gaussian Multiplicative Chaos via a high dimensional CLT with low rank increments
The Gaussian multiplicative chaos (see figure), often abbreviated as "GMC", is a key object in many diverse contexts, for instance in quantum field theory (eg. 2D Liouville quantum gravity) and mathematics (eg. Riemann zeta function, and random matrices). It is a random fractal measure, first constructed by Kahane in 1985 to study intermittency in fluid turbulence. However, the construction relied crucially on Gaussian theory, and was only recently extended to non-Gaussian settings.
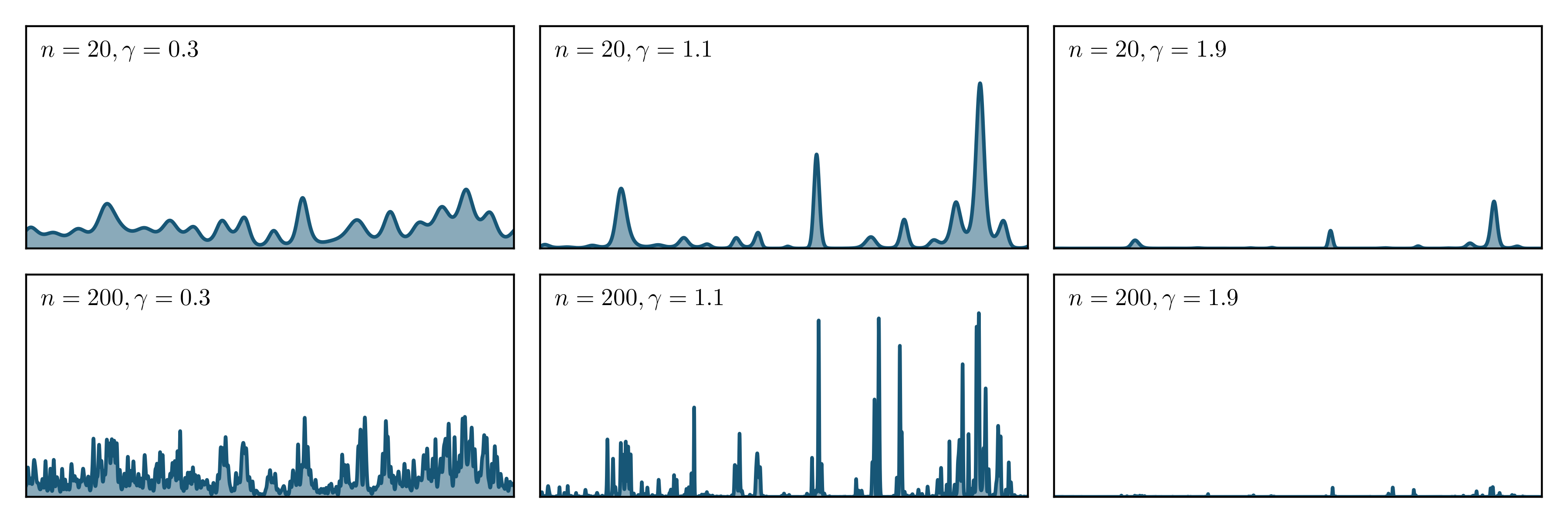
Gaussian multiplicative chaos (of intermittency parameter $\gamma$) for the random Fourier series with $n$ terms.
As is common in probability, the introduction of a non-Gaussian limit objects is accompanied by questions of universality, i.e., "is the non-Gaussian object the same/related to the Gaussian version" (the central limit theorem is a classic example). Although answering this for the GMC is a beautiful and natural problem, it turns out to be even more interesting since it involves carefully understanding how high-dimensional random vectors, with rank-one covariances, can "homogenize" to a Gaussian variable, clearly a fundamental question in high-dimensional probability and statistics. We answer this in a general, and near-optimal sense, allowing us to improve upon prior, and widely used, results in the literature. For the GMC, our CLT implies that the non-Gaussian and Gaussian versions are mutually absolutely continuous (under suitable couplings), a key first step in understanding the universality of any class of random measures.
3. Gaussian to log-normal transition for independent sets on a percolated hypercube
Combinatorial optimization problems, such as the Hamiltonian cycle, traveling salesman, MAX-SAT, MAX-CUT, and the largest independent set, have been extensively studied in computer science literature and form the foundation of complexity theory. However, a significant limitation of this theory is its focus on the worst-case scenario. In contrast, the average-case analysis of these problems, which is arguably more relevant, has only recently gained traction and is now a vibrant area of research in probability and computer science theory. Interestingly, many of these problems are connected to statistical physics and the phenomena of phase transitions through the language of Gibbs measures.
Consider a hypercube, i.e., a graph whose vertices are the binary strings of a fixed length $d$, and two vertices are adjacent if their corresponding strings differ in exactly one bit (see the figure for the $d = 4$ case). The largest independent set problem on the hypercube is a problem with a long history, starting with the work of Korshunov and Sapozhenko, counting the number of independent sets, as well as describing the structure of a typical independent set. The structure is as follows. Let us divide the hypercube into an even and an odd side, depending on the number of bits that equal 1. Then, choose one side uniformly, and pick a $\mathrm{Poisson}(1/2)$ number of them. This is called the "defect" (in the figure below, the even side at the bottom is the defect side with 2 defects in red). Then remove all neighbors of defect vertices, and choose a random subset of the other side among the vertices that survive. These vertices together form a uniform independent set.
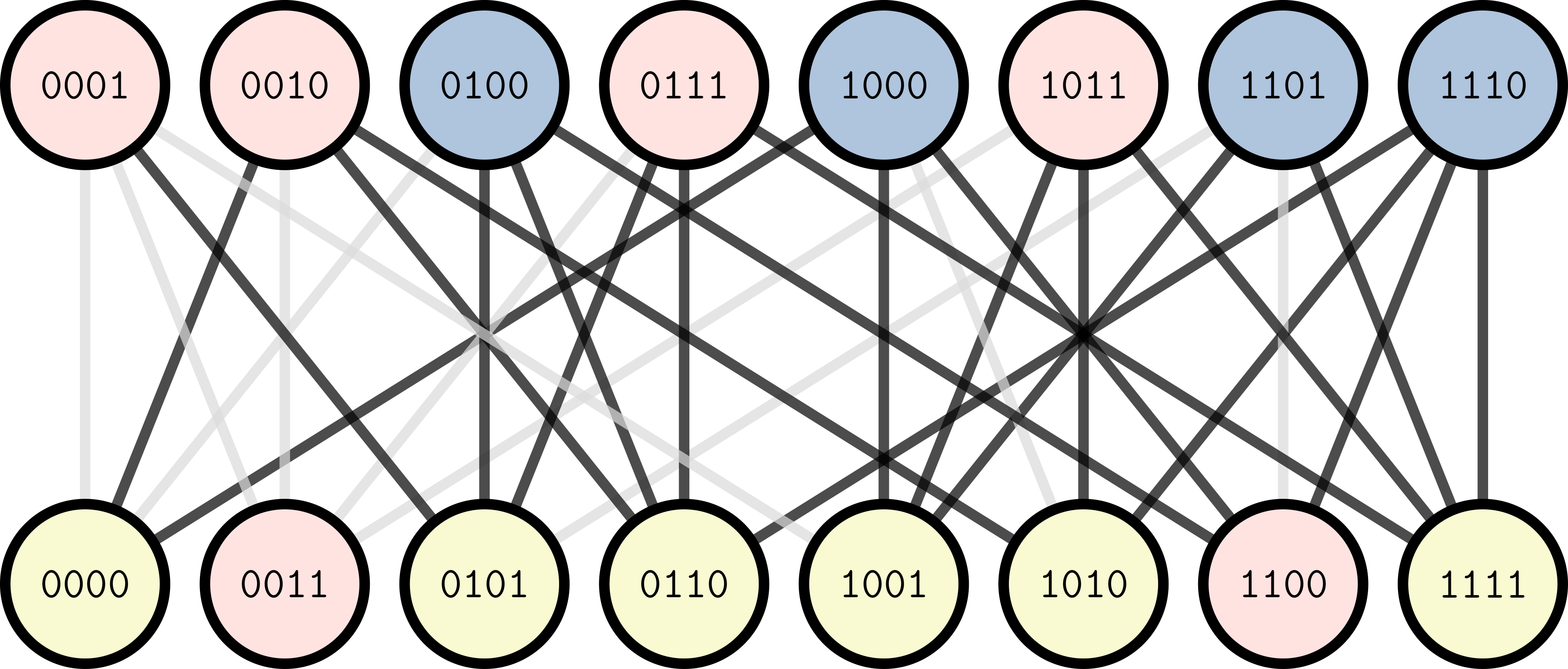
An instance of a percolated hypercube of dimension 4, drawn to emphasize the bipartite structure. The red vertices form an independent set.
Of course, there is no randomness in the problem description, but suppose, we now remove some constraints randomly. Say we drop each edge with probability $p$, independently. In the figure, the solid black edges remain, and the gray edges have been dropped. In this disordered setting, how does the number of independent sets (now random) behave? How does a typical independent set look like? These questions were first asked in 2022 by a paper of Kronenberg and Spinka [KS] , referring to this model as the percolated hypercube. It turns out that there is a sharp transition at $p = 2/3$, where the count of independent sets transition from being a Gaussian to being log-normal. This was conjectured in [KS], and we establish this concretely in our paper, employing a very different approach compared to earlier works in this direction, which relied on the computation of moments. Our approach proceeds via building a probabilistic understanding of this model, also lending its way to the description of the structure of typical independent sets. It turns out that at $p = 2/3$, the defect side can no longer be picked uniformly, but instead depends crucially on the realization of the percolation.
2. Characterizing Gibbs states for area-tilted Brownian lines
Models in statistical physics often give rise to collections of random curves, called line ensembles. As an example, consider the classical Solid-on-Solid model, which seeks to study the interface between two solids. More specifically, it studies the interface between the two phases in a magnet whose, say, bottom surface is magnetized to be spin "down", and rest of the magnet is spin "up" (this is not representative of the actual physics of the system, the true interpretation and model comes from quantum mechanical considerations). Due to a phenomenon called entropic repulsion from the bottom surface, the interface will actually rise up from the bottom surface, resulting in many large level curves, which is a curve at constant height (think of a contour in geographic maps). Many important quantities of interest may then be examined by understanding the level curves of this object. The behavior of these curves is of great interest, and suitable probabilistic objects have been defined which capture that behavior. This is the area-tilted line-ensemble, a collection of ordered, nonintersecting random curves, which is the primary focus of the paper.
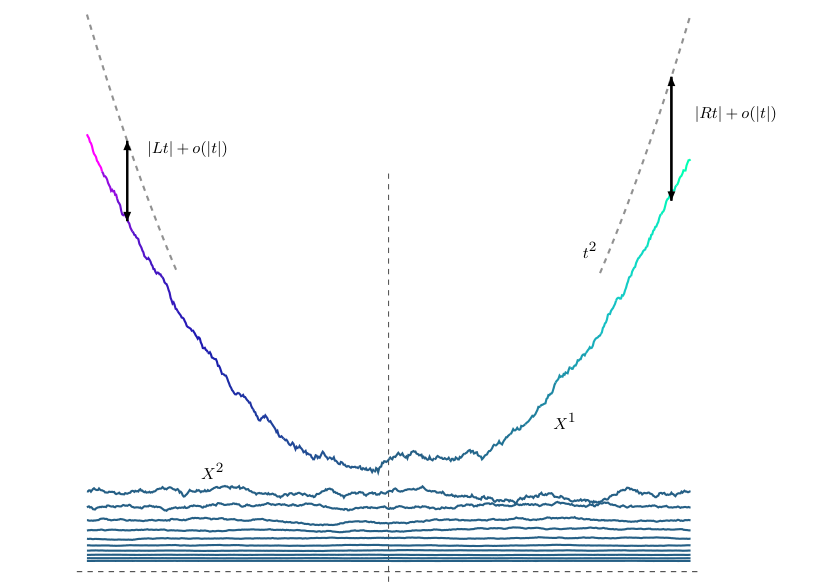
A quadratically growing area-tilted ensemble. Observe how only the first curve can grow.
To elaborate further, this ensemble is specified in terms of its finite domain marginals. The so-called area-tilted Brownian Gibbs property describes this behavior and is derived from the description of the Solid-on-Solid model. It is a known, nontrivial, fact that this ensemble is a well-defined mathematical object (nothing blows up or vanishes under the scaling operations performed to reach it). Until now, only one ensemble was known which satisfied the said Gibbs property. In this paper, we succeed in finding all of them. Perhaps surprisingly, there is an infinite family of such ensembles (yes, an infinite family of families of infinitely many lines) parametrized by two numbers $L, R$ (representing left and right "rates of growth") such that their sum is $L + R < 0$. The original ensemble corresponds to $L = R = -\infty.$ See the figure for an example.
1. Universality in prelimiting tail behavior for regular subgraph counts in the Poisson regime
A graph is a mathematical object used to describe relationships between things. Since real-world graphs are very complex, it is often of interest to understand the nature of random graphs. The most famous model of random graphs is the celebrated Erdős–Rényi model, which is created by taking $n$ vertices, and joining each pair with probability $p$ independently - let $G$ be such a random graph. Think of this as $n$ people, and any two people know each other with probability $p$ independently of the others. For $p = 0.1$ say, each vertex is connected to $0.1 n$ many other vertices on average, which is a huge number. Many applications require this average degree, i.e., the number of other vertices a given vertex is connected to, to be constant, say 5. A moment's thought then reveals that one may seek to emulate this behavior by modifying $p$ with $n$, precisely by choosing something like $p = 5/n$. This is a so-called sparse Erdős–Rényi graph.
Several basic questions can be asked about this model. Among them, of enormous importance is the notion of subgraph count. For example, I can ask "How many triangles are there in this graph?" by which I mean "How many groups of 3 people A, B, C are there such that all of them know each other?". Our understanding of how exactly this count behaves (on a very precise level) was actually open until very recently. But as one may imagine, it is possible to ask this question for any configuration, say the count of four people A, B, C, D forming a "square". In this spirit, this paper provides a generalization of the recent triangle result, extending it to every possible "regular" subgraph, which is every configuration where each person knows the same number of people among the rest (the square example is one such - everyone knows 2 others in the group).